Scatter Plots and Math - Replicating Radar Research
- Gavin Tolometti
- Feb 3, 2020
- 6 min read
I have been reading synthetic aperture radar (SAR) research papers to decide how to best interpret the quantified radar data of the Holuhraun lava flow-field. Currently, I have produced histograms showing the distribution and mean of CPR from each lava flow type in the lava flow-field. It has allowed me to see how the surface roughness of the lava flow types compare to each other. Some of the lava flow types return similar CPR values, making them almost indistinguishable under radar. I wanted to see if these lava flow types could be distinguished by studying the polarization properties that are used to calculate CPR. For context, polarimetry radar signals can be horizontally (H) polarized or vertically (V) polarized. Depending on the combination of polarization signals emitted and received, different information can be gathered about the physical and electrical properties of planetary surfaces. E.g. HHVV is means the emitted signal was horizontally polarized and the received signal was vertically polarized. One paper that uses polarized radar properties and CPR to understand the surface roughness backscatter of lava flows is Campbell (2012).
In Campbell (2012), he seeks to understand what scattering mechanisms and surface features are responsible for >1 CPR values for the Maxwell Montes on Venus, lunar crater ejecta and walls, and the blocky SP Flow in Arizona. He uses data collected by the quad-pol NASA/JPL AIRSAR instrument, which has a pixel resolution of ~12 m/pixel to determine what scattering mechanisms are present at the SP Flow. He focuses on part of the flow near the crater (Figure 1), extracting pixel data from the AIRSAR scene image (CM6453).

Figure 1. Modified version of Campbell (2012) figure showing the area of focus in his research. The red outline covers the area where radar pixel data was extracted. The image is a CPR image overlying a total backscatter (S1) image.
With the data he extracted, he generated four plots to determine what the dominant scattering mechanism is for the rough surface of SP Flow. The plots are shown below, comparing CPR to radar polarization ratios, and the beta (β) value.

The main points to take away from these plots, which are discussed in Campbell (2012) are the following:
A. Histogram showing the distribution of CPR in the study area.
B. No correlation between CPR and HH/VV ratio, indicating dihedral scattering.
C. Strong positive correlation between CPR and HV/HH ratio, which is expected for scattering models that describes how signals are single- or double-bounced off surfaces.
D. Negative correlation between CPR and β. This negative correlation is consistent with the decline in HH- and VV-polarized returns with increasing dipole-scattering mechanisms.
I wanted to see if the lava flow types at Holuhraun showed any of these CPR-polarization ratio correlations. Before I started that, I had to see if I could replicate the plots by Campbell (2012). I began by downloading the data products available on the JPL AIRSAR database. This data is publicly available by the way (AIRSAR Precision Imagery). Issue is you need to know how to process the data into a readable format. What I did was download the L-band radar data labelled as 'ldata'. The data needed to be opened and converted into text files before being processed and converted into images. I ran the 'ldata' file through an IDL script, which opened the data and calculated the Stokes matrix values (equations below). Now I was not needing the Stoke matrix values. What I wanted were the polarization products that were used to calculate the Stoke matrix (equations below). So it was not as simple as I thought. It looked like I needed to do some old fashioned equation rearranging to get the polarization products.
W11 = 1/4[HHHH + VVVV + 2(HVHV)]
W12 = 1/4[HHHH - VVVV]
W13 = 1/2(HHHVR) + 1/2(HVVVR)
W14 = -1/2(HHHVI) - 1/2(HVVVI)
W22 = 1/4[HHHH + VVVV - 2(HVHV)]
W23 = 1/2(HHHVR) - 1/2(HVVVR)
W24 = -1/2(HHHVI) + 1/2(HVVVI)
W33 = 1/2(HVHV) + 1/2(HHVVR)
W34 = -1/2(HHVVI)
W44 = 1/2(HVHV) - 1/2(HHVVR)
I started the equation rearaanging by looking to see which Stoke matrix contained HHHH, VVVV, and HVHV in their equations, since these products were used by Campbell (2012). From the equation list above, W11, W12, W22, W33, and W44 contain these products. I then began re-arranging the Stoke matrix equations to isolate HHHH, VVVV, and HVHV. To save you all from the scribbles and failed re-arrange equation tests in my notebook, I have only shown the correct equations.
Calculating HVHV
Since W11 and W22 both have like-polarized echo data we can use them to calculate HVHV.
W11 - W22
=> 1/4[HHHH + VVVV + 2(HVHV)] - 1/4[HHHH + VVVV - 2(HVHV)]
=> 1/4(HHHH) + 1/4(VVVV) + 1/2(HVHV) - 1/4(HHHH) - 1/4(VVVV) + 1/2(HVHV)
HHHH and VVVV are cancelled out, leaving only HVHV polarization echo data.
=> W11 - W22 = HVHV
Calculating HHHH
W11 + 2W12 + W22
=> 1/4[HHHH + VVVV + 2(HVHV)] + 2*(1/4[HHHH - VVVV]) + 1/4[HHHH + VVVV - 2(HVHV)]
=> 1/4(HHHH) + 1/4(VVVV) + 1/2(HVHV) + 1/2(HHHH) - 1/2(VVVV) + 1/4(HHHH) + 1/4(VVVV) - 1/2(HVHV)
VVVV and HVHV are cancelled out, leaving only HHHH polarization echo data.
=> W11 + 2W12 + W22 = HHHH
Calculating VVVV
W11 - 2W12 + W22
=> 1/4[HHHH + VVVV + 2(HVHV)] - 2*(1/4[HHHH - VVVV]) + 1/4[HHHH + VVVV - 2(HVHV)]
=> 1/4(HHHH) + 1/4(VVVV) + 1/2(HVHV) - 1/2(HHHH) + 1/2(VVVV) + 1/4(HHHH) + 1/4(VVVV) - 1/2(HVHV)
HHHH and HVHV are cancelled out, leaving only VVVV polarization echo data.
=> W11 - 2W12 + W22 = VVVV
Calculating HHVVR
I needed HHVVR to calculate β̞. β̞ is a normalized ratio of the HHVV polarimetric echo, calculating using the following equation:
R[HHVV] / (√(HHVVR)
HHVVR was calculated using W33 and W44 Stokes matrix.
W33 - W44
=> 1/2[HVHV + HHVVR] - 1/2[HVHV - HHVVR]
=> 1/2HVHV + 1/2HHVVR - 1/2HVHV + 1/2HHVVR
HVHV is cancelled out of the equation
=> W33 - W44 = HHVVR
Replicating Campbell (2012) Plots
With the HHHH, VVVV, and HVHV polarization products calculated using the available Stoke matrix data, I was able to use the raster calculator tool in ESRI ArcGIS to create the images I needed to replicate the scatter plots published by Campbell (2012). Using the "Extract Value to Table" tool in ArcGIS, I extracted the value of each pixel within the area studied by Campbell.
I re-created the plots using Python 2 and 3 matplotlib scripts since it allowed me to manipulate the data and format the plots to be readable.




I was able to replicate the CPR histogram (top left graph) and HH/VV plot (top right graph) quite well. I had issues with the HV/HH and Beta plots because I could not plot the same trend reported by Campbell (2012). The HV/HH plot (bottom left graph) was close to Campbell (2012), however the CPR values started to remain constant around 1.4 instead of increasing to 1.5. At this time, it is difficult for me to say why I am not seeing the same correlation. One reason could be how I extracted the data from the radar images, and sorted and plotted them from text files. Another reason could be there are steps I am missing from Campbell (2012). I had to plot these based off an assumption on how I thought Campbell plotted them. It appears I am only able to replicate two plots. I ran into a similar issue when I decided to use radar polarization data from a spiny lava flow from the Holuhraun lava flow-field in Iceland.


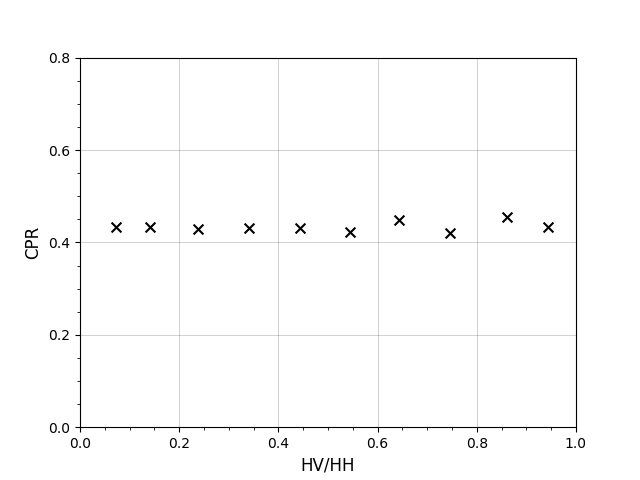

There are no trends between the CPR and radar polarization data. It is most likely because these ratios are useful for determining the scattering properties of lava flows returning CPR values greater than one, and are not applicable to lava flows returning lower CPR. This is only an assumption, and may change as I read more research papers and consult with my supervisor.
If anyone has any thoughts on these plots and reasons why I am not seeing any similar correlations in my Holuhraun radar data, I would be happy to hear from you! You can contact me through my website 'Contacts' page, Twitter (@GavinOnTheMoon), or email me at gtolomet@uwo.ca.
On another note, my manuscript titled "Radar Interpretations of Lava Flows Using Surface Roughness" is now in the decision process of being sent back for revisions. I am hoping to get a response this week! Follow to stay tuned :D
See you all next time!
Reference
Campbell, B. A. (2012). High circular polarization ratios in radar scattering from geologic targets. Journal of Geophysical Research: Planets, 117(E6).






Comments